The Rasch model in e-asTTle
This section explains some of the underlying test theory used in e-asTTle.
For a simplified explanation, see Guidelines on creating effective Custom or Adaptive tests.
An explanation of the multi-faceted Rasch model used in scoring writing can be found here
Comparison to conventional testing
In classical test theory, percent correct is used for scoring. An issue with this approach – which the Rasch model attempts to solve – is that the difficulty of the test isn’t considered.
Consider two reading tests. The first has 32 questions, all at curriculum Level 2. The second has 24 much harder questions, entirely at curriculum level 4. The easy test is given to Johnny at the beginning of the year, and the harder test, at the end of the year. Johnny got all questions right on the first test, but only eight questions correct on the second. Has Johnny improved?
Using classical test theory, Johnny gets a 100% score at the beginning of the year, and 33% at the end of the year. Of course, it is not reasonable to use the percentages to assess Johnny’s progress. It is obvious the tests are not comparable, and when using percentages, there is no way of working out what progress Johnny has made. The Rasch model provides a score for each test, which is still essentially based on percent-correct – however, it is adjusted for the test’s difficulty. These scores can be used for comparison, even across test papers that are very different.
e-asTTle uses the Rasch model to assign difficulty values to test questions and equivalent ability levels to students. The difficulty values are later translated to curriculum levels.
Probabilities and the Rasch model
The Rasch model is about probabilities. It is based on the idea that we can model how likely it is a student responds correctly to a test question based on the difference between test question difficulty and student ability. (Wright, B. & Stone, M. (1979). Best test design).
Mathematically, the logistic curve is used to model how the probability of a correct response relates to how far apart the student and question are in terms of difficulty.
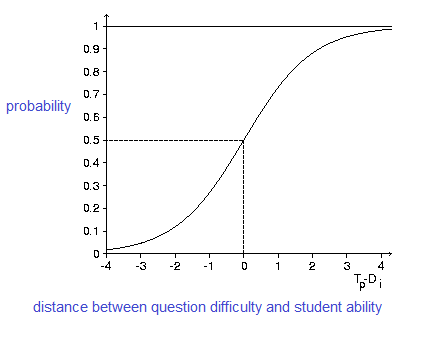
If the question difficulty is higher than the ability of the student, we would say the student is < 50% likely to answer it correctly. However, if the student’s ability is higher than the question, the student has a > 50% probability of answering it correctly. If the ability and difficulty are exactly equal, the probability is 50%.
How are questions assigned difficulties?
Periodically, the responses to all questions in e-asTTle are extracted into a huge matrix. The raw scores (i.e percent-correct) for each student and for each question are calculated.
For each question and each student, we work out the ratio between percent-correct and percent-incorrect. This is transformed using a natural logarithmic transformation. Question difficulties are adjusted for the spread of abilities, and person abilities are adjusted for the width of the test they sat. Then, Joint Maximum Likelihood Estimation is used to iterate through the matrix and fit it towards a logistic curve such as the above.
At the end of these transformations, all questions will be assigned a logit value – usually between -5 and +5 – to indicate their relative difficulty. These values are put back into e-asTTle and used to score students.
How are students assigned scores?
During scoring, students are assigned a value between -5 and +5 based on the difficulty values of the questions they answered.
A student with ability 0.0 has a 50% probability of correctly answering a question of 0.0 difficulty. The ability assigned is a best estimate of the student’s ability to correctly answer half of the questions at that difficulty level.
A similar procedure applies to deep, surface and strand scoring. However, here only a subset of questions is used in the calculation process. For example, only Algebra questions are included when generating an Algebra score.
The value between -5 and +5 is transformed to the e-asTTle scale (mean, 1500 and standard deviation, 100) to make it easier to interpret.
How do the scores map to curriculum levels?
Once the questions have assigned difficulty values, a sample of questions is taken and placed in difficulty order – that is, from easiest to hardest. A panel of teachers and curriculum experts decide the cut-off points for each curriculum level.
More information on the Rasch model
- Related information

